Interaction with Geometry
CindyScript can interact in different ways with a geometric drawing that was created with Cinderella. We already saw that it can read the numerical data and appearance of geometric elements. However it can also change the position of the free elements of a construction. CindyScript may even inquire and change the construction sequence by creating and deleting new geometric elements.
Moving Elements
The calculations within CindyScript can be used to control the positions of free elements in a Cinderella construction.
One way of doing this is to explicitly set the position information of a free element.
For instance, if A is a free point, the line A.xy=[1,1] sets this point to the coordinates [1,1].
Another way of moving an element is with the moveto operator.
Moving a Free Element: moveto(‹geo›,‹pos›)
Description:
In this operator, ‹geo› is a free geometric object and ‹pos› (usually a vector) describes a position to which this object should be moved.
Calling this operator simulates a move for this geometric object.
If ‹geo› is a free point, then ‹vec› can be a list [x,y] of two numbers or a list [x,y,z] of three numbers.
The first case is interpreted as Euclidean coordinates, while the second case is interpreted as homogeneous coordinates and sets the point to [x/z,y/z].
If ‹geo› is a free line, then ‹vec› has to be a list of three numbers [a,b,c], and the line is set to the line described by the equation a∗x + b∗y + c = 0.
Examples: The following code lines summarize possible ways to move geometric elements (we also include the possibilities of moving elements by accessing their data fields):
[{name:"A", type:"Free", pos:[7,5]}] // A is a free pointmoveto(A, [1,4]); // moves A to Euclidean coordinates [1,4] A.xy
[1, 4]
A.xy = [2,3]; // moves A to Euclidean coordinates [2,3] A.xy
[2, 3]
A.x=5; // sets the x coordinate of A to 5, A.xy // leaves the y coordinate unchanged
[5, 3]
A.y=8; // sets the y coordinate of A to 3, A.xy // leaves the x coordinate unchanged
[5, 8]
moveto(A,[2,3,2]); //moves A to homogeneous coordinates [2,3,2] A.xy
[1, 1.5]
A.homog=[5,3,4]; //moves A to homogeneous coordinates [5,3,4] A.xy
[1.25, 0.75]
[{name:"a", type:"FreeLine", pos:[1,1,1]}] // a is a free linemoveto(a,[2,3,4]); //moves a to homogeneous coordinates [2,3,4] 2 * a.homog / a.homog_1
[2, 3, 4]
a.homog=[5,4,3]; //moves a to homogeneous coordinates [5,4,3] 5 * a.homog / a.homog_1
[5, 4, 3]
[{name:"B", type:"Free", pos:[0,0]},
{name:"b", type:"Through", args:["B"], dir:[1,2,0]}]b.slope
2
b.slope=1; //sets the slope of the line to 1 b.homog / b.homog_1
[1, -1, 0]
[{name:"M", type:"Free", pos:[0,0]},
{name:"C", type:"CircleMr", args:["M"], radius:7}]C.radius
7
C.radius=2; //sets the radius of the circle to 1 C.radius
2
C.matrix / C.matrix_1_1
[[1, 0, 0], [0, 1, 0], [0, 0, -4]]
Handles to Objects
Who has moved: mover()
Description: This operator gives a handle to the element that is currently moved by the mouse.
Elements close to the mouse: elementsatmouse()
Description: This operator gives a list with handles to all the elements that are close to the current mouse position.
Example: The following script is a little mean. Putting it into the mouse move slot will make exactly those elements disappear that are close to the mouse. They reappear if the mouse moves away again.
skip test: elementsatmouse not implemented yet
apply(allelements(),#.alpha=1); apply(elementsatmouse(),#.alpha=0); repaint();
Incidences of an object: incidences(‹geo›)
Description:
This operator returns a list all the elements that are generically incident to a geometric element ‹geo›.
Getting an element by name: element(‹string›)
Description:
This operator returns the geometric object identified by the name given in ‹string›.
Example:
The element operator is necessary for situations where the element name is not a valid variable identifier or already used by a user-defined or built-in name.
For example, if you try to access the color of a line having the name i, you cannot write i.color=[1,1,1] as i is reserved for the complex unit.
[{name:"i", type:"Free", pos:[1, 2]}]i
0 + i*1
2*i
0 + i*2
i.color
___
Instead, you use:
element("i")i
2*element("i")[2, 4]
element("i").color[1, 0, 0]
Creating and Removing Elements
Creating a free point: createpoint(‹string›,‹pos›)
Description:
This operator creates a new point with label ‹string›.
The point will beset to position ‹pos›.
If an element with this name is already exists then no new element is created.
However, if there already exists a free point with this name, then this point is moved to the specified position.
Creating a geometric element: create(‹list1›,‹string›,‹list2›)
Description: With this operator, it is possible to generate arbitrary geometric elements that are functional in a geometric construction. Due to the fact that algorithms may create multiple outputs several subtleties arise. This function is meant for expert use only.
The first list contains a list ‹list1› of element names for the generated output objects of the algorithm.
‹string› is the internal name of the geometric algorithm.
The second list ‹list2› is a list of the parameters that are needed for the definition.
Through modifiers, it is possible to specify attributes of the geometric elements.
The corresponding geometric element is returned. If ‹list1› contained multiple entries, then also a list of geometric elements is returned.
The following table shows a few possible creation statements.
only CindyJS: Cinderella uses different names for its algorithms
[]
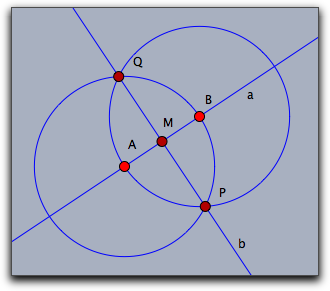
create(["A"],"Free",[[1,1,1]]); create(["B"],"Free",[[4,3,1]]); create(["a"],"Join",[A,B]); create(["X"],"CircleMP",[A,B]); create(["Y"],"CircleMP",[B,A]); create(["P","Q"],"IntersectionCircleCircle",[X,Y]); create(["b"],"Join",[P,Q]); create(["M"],"Meet",[a,b]); allelements()
[A, B, a, X, Y, P__Q, P, Q, b, M]
This sequence of statements creates the fully functional construction shown below.
Observe that in the sixth statement when two circles are intersected,
the approach above gives two output names corresponding to the two points of intersection.
Internally there is yet another element (names P__Q as can be seen from the list of all elements) which represents both of these together.
You can find the valid parameters for elements by constructing them manually and using the algorithm and inputs functions described below.
Creating a geometric element with no given name: create(‹string›,‹list2›)
Behaves as the 3-arity create, but the list of element names as first arguments is not given and the names of the elements are chosen by CindyJS.
If an algorithm (such as "IntersectionCircleCircle") gives multiple geometric objects then a list of the created elements is returned instead of a single element. However, if a modifier pos is specified, then only the point closest to pos is created and returned.
If too many arguments are given in ‹list2›, then those arguments are ignored and the last given argument will be interpreted as a modifier pos, if pos has not been defined yet.
Removing a geometric element: removeelement(‹geo›)
Not available in CindyJS yet!
Description: Removes a geometric element together with all its dependent elements from a construction.
Input elements of an element: inputs(‹geo›)
Description:
This operator returns a list all the elements that are needed to define the object ‹geo›.
These may be other geometric, elements, numbers or vectors.
For a free point, the input is its homogeneous position.
[{name:"A", type:"Free", pos:[0.1, 0.2]}]inputs(A)
[[0.1, 0.2, 1]]
For an object which is fully determined by other geometric elements, the inputs are these defining elements. They are given as geometric elements, not as name strings.
[{name:"A", type:"Free", pos:[0, 0]},
{name:"B", type:"Free", pos:[1, 0]},
{name:"a", type:"Join", args:["A", "B"]}]inputs(a)
[A, B]
ispoint(inputs(a)_1)
true
isstring(inputs(a)_1)
false
Algorithm of an element: algorithm(‹geo›)
Description:
This operator returns a string that resembles the algorithm of the definition the object ‹geo›.
Modifiers:
The modifier compatibility can be set to the string "Cinderella"
in order to obtain names in a way compatible with what Cinderella would return.
That mapping is not perfect due to some implementation details,
but this makes a best effort to come as close as possible to Cinderella output.
Example:
For this example, we first define a construction of a perpendicular bisector, as shown in this figure:
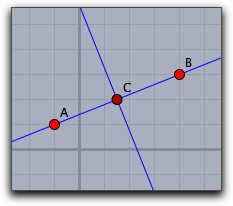
[{name:"A", type:"Free", pos:[-1,-1]},
{name:"B", type:"Free", pos:[4,-3]},
{name:"a", type:"Join", args:["A","B"]},
{name:"C", type:"Mid", args:["A","B"]},
{name:"b", type:"Orthogonal", args:["a","C"]}]Now the following piece of code generates all the information contained in that construction sequence.
allelements()
[A, B, a, C, b]
only CindyJS: Cinderella uses different names for its algorithms
data = apply(allelements(),([[#.name],algorithm(#),inputs(#)])); forall(data, print(#));
[[A], Free, [[1, 1, -1]]] [[B], Free, [[1, -0.75, 0.25]]] [[a], Join, [A, B]] [[C], Mid, [A, B]] [[b], Perp, [a, C]]
data == [ [["A"], "Free", [[1, 1, -1]]], [["B"], "Free", [[1, -0.75, 0.25]]], [["a"], "Join", [A, B]], [["C"], "Mid", [A, B]], [["b"], "Perp", [a, C]] ]
true
As written above, Cinderella uses different names here:
apply(allelements(), algorithm(#, compatibility->"cinderella"))
["FreePoint", "FreePoint", "Join", "Mid", "Orthogonal"]
Accessing Element Properties
Element properties like color, size, etc.
are conveniently accessible via operators like .color, .size etc.
However, elements have by far more properties.
All of them can be generically accessed by the following operators.
List all inspectable properties: inspect(‹geo›)
Not available in CindyJS yet!
Description: Returns a list of names of all private properties of a geometric element.
Example:
The operator inspect(A) applied to a the free point A returns the following list of property names.
skip test: inspect not implemented yet
inspect(A)
[name,definition,color,color.red,color.blue,color.green,alpha,visibility, drawtrace,tracelength,traceskip,tracedim,render,isvisible, text.fontfamily,plane,pinning,incidences,labeled,textsize,textbold,textitalics, ptsize,pointborder,printname,point.image, point.image.media,point.image.rotation,freept.pos]
Accessing an inspectable property: inspect(‹geo›,‹string›)
Not available in CindyJS yet!
Description: Accesses an arbitrary inspectable property.
Example:
One can access the color of a point A by inspect(A,"color")
Setting an inspectable property: inspect(‹geo›,‹string›,‹data›)
Not available in CindyJS yet!
Description: Setting the value of inspectable property.
Example:
One can set the color of a point A to white by inspect(A,"color",(1,1,1))
Forcing a repaint operation: repaint()
Not available in CindyJS yet!
Description:
This operator causes an immediate repaint of the drawing surface.
This operator is meant to be used whenever a script has updated a construction and wants to display the changes.
It is not allowd to use this operator in the draw or in the move slot.
Forcing a delayed repaint operation: repaint(‹real›)
Description:
As repaint but with a time delay of as many milliseconds as given by he parameter
Points on a locus: locusdata(‹locus›)
Not available in CindyJS yet!
Description:
This operator returns a list of points in xy-coordinates that are all on a locus given by the name ‹locus› of a geometric element.
Creating a continuity checkpoint: continuefromhere()
Description:
Usually if a mouse moves a geometric element, and then a script moves the same element to another position (and does not move any other element), then both of these moves are combined. If one of them encounters a singular situation, then the whole operation will be considered singular, and subsequent moves will continue from the last non-singular situation before that move.
Sometimes however it is desirable for a script to deliberately split that operation: move to some (preferrably non-singular) situation in a controlled way, then create a checkpoint there so that subsequent moves will start from this situation instead of the one before the mouse move to some singular situation.
